天不言而四时行,地不语而百物生。
介绍
排序是指按特定顺序(数字或字母顺序)排列列表中的项目。排序通常与搜索一起使用。
如果在视觉上和算法上对列表进行了排序,那么在给定列表中搜索元素(称为键)通常会更容易。
有很多方法(算法)可以对给定的元素列表进行排序。归并排序是一种更流行、更有效的方法。
在本文中,我们将看到合并排序背后的逻辑,在 JavaScript 中实现它,并在操作中对其进行可视化。最后,我们将在空间和时间复杂度方面将归并排序与其他算法进行比较。
理解归并排序背后的逻辑
合并排序使用分而治之的概念对给定的元素列表进行排序。它将问题分解为更小的子问题,直到它们变得简单到可以直接解决。
以下是归并排序的步骤:
- 将给定的列表分成两半(对于具有奇数个元素的列表,大致相等的一半)。
- 继续以相同的方式划分子数组,直到只剩下单个元素数组。
- 从单元素数组开始,合并子数组,以便对每个合并的子数组进行排序。
- 重复第 3 步,最终得到一个排序数组。
让我们来看看合并排序如何在数组上工作,例如 [4, 8, 7, 2, 11, 1, 3]:
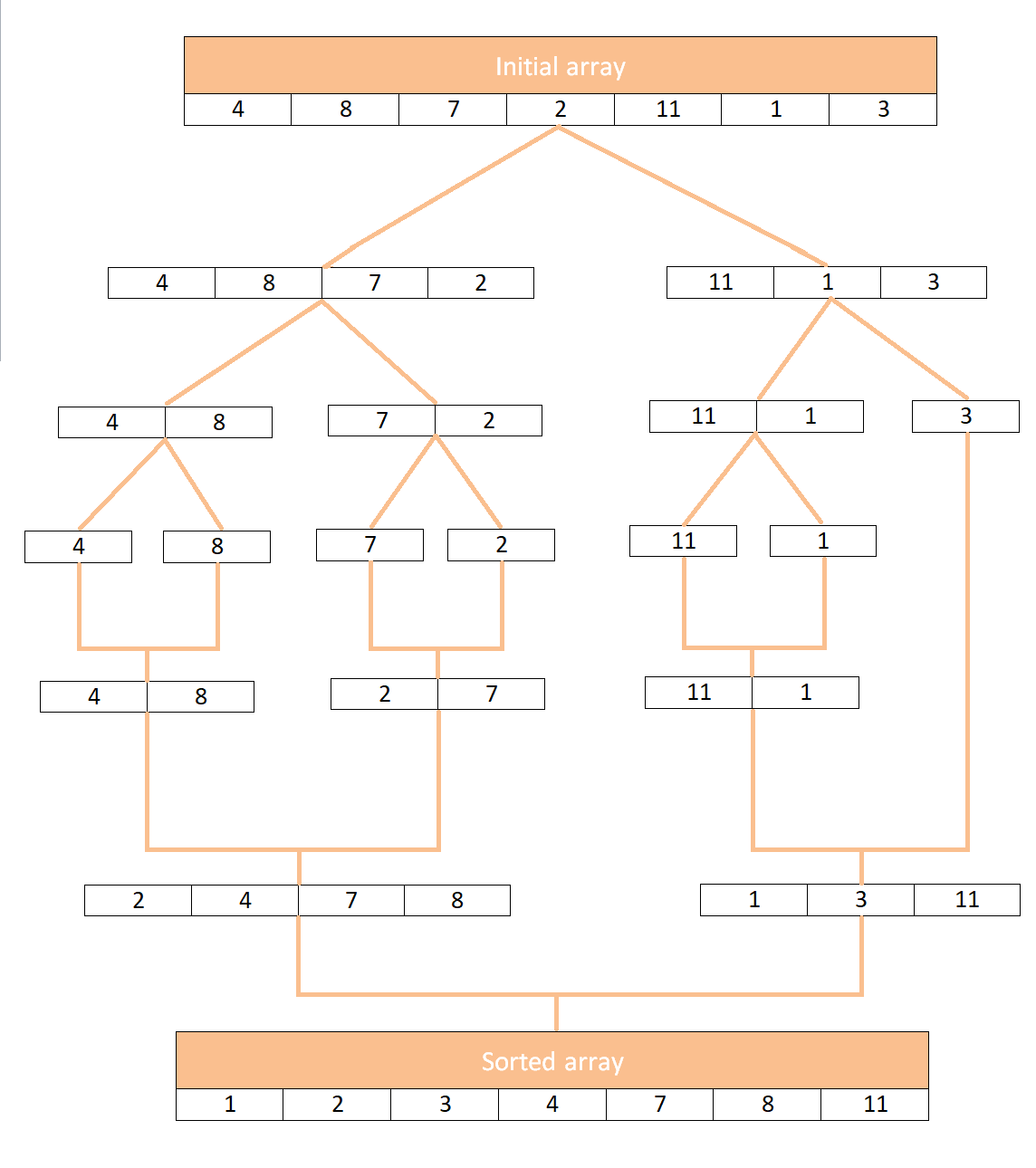
JavaScript 中合并排序的实现
让我们首先将 merge()两个已排序的子数组编写为一个已排序数组的代码。记住两个子数组都已经排序非常重要,我们只是使用该 merge()函数将它们组合起来。
我们可以通过遍历这两个子数组并一一添加元素来完成此操作,以便对结果数组进行排序:
1 | function merge(left, right) { |
在此函数中,我们采用两个已排序的子数组 (left, right)并将它们合并以获得一个已排序的数组。首先,我们创建一个空数组。稍后,我们选择 left 和 right 子数组中最小的未选择元素中的较小者,并将它们推入空数组。我们只需要检查 left 和 right 子数组中的第一个元素,因为它们都已排序。
在执行此操作时,我们从子数组中删除选取的元素(这是使用 shift() 函数实现的)。我们继续这个过程,直到其中一个子数组变空。之后,我们将非空子数组的剩余元素(因为它们已经排序)推送到主数组中。
由于我们现在有合并两个排序数组的代码(分而治之的征服部分),让我们为我们的合并排序算法编写最终代码。这意味着我们需要不断拆分数组,直到得到只包含一个元素的数组:
1 | function mergeSort(array) { |
在这里,我们确定中点并使用 splice() 函数将数组拆分为两个子数组。如果有奇数个元素,则左边的元素数量较少。我们一直在进行除法,直到剩下单个元素数组 (array.length < 2)。之后,我们开始使用之前编写的 merge() 函数组合子数组。
现在我们已经有了代码,让我们看看在前面的例子中运行函数的输出:
1 | array = [4, 8, 7, 2, 11, 1, 3]; |
归并排序的效率
合并排序的最坏情况时间复杂度为 O(nlogn),与快速排序的最佳情况时间复杂度相同。说到速度,归并排序是目前最快的排序算法之一。
与快速排序不同,合并排序不是就地排序算法,这意味着它会占用除输入数组以外的额外空间。这是因为我们使用辅助(辅助)数组来存储子数组。归并排序的空间复杂度是O(n)。
合并排序的另一个优点是它非常适合多线程,因为每个各自的一半都可以自己排序。减少合并排序运行时间的另一种常见方法是在我们到达相对较小的子数组(~7)时停止并使用 插入排序对它们进行排序。
这样做是因为插入排序在小数组或接近排序的数组上表现得非常好。比更具全球效率的同行要好得多。
总结
在本文中,我们看到了归并排序算法背后的逻辑,如何在 JavaScript 中实现它,并了解了它的性能。它是基本的排序算法之一,对于给出一个清晰的分治策略示例非常有用。
参考
关注【公众号】,了解更多。

赞赏一下 坚持原创技术分享,您的支持将鼓励我继续创作!
 支付宝打赏
支付宝打赏 微信打赏
微信打赏